Marcus Frings
The Golden Section in Architectural Theory
Marcus Frings, "The Golden Section in Architectural Theory", Nexus Network Journal vol. 4 no. 1 (Winter 2002), pp. 9-32; ISSN 1590-5896 (Print) / 1522-4600 (Online)
Abstract
The never-ending – but always young – discussion about the Golden Section in architecture never lacks a hint at Luca Pacioli and architectural theory. But what it always lacks is a thorough study of the Golden Section in architectural theory. This paper aims to present this analysis. Marcus Frings traces the Golden Section from the mathematical and rather theoretical character of Pacioli’s concept, the the treatises of Alberti, Serlio, and Palladio, to Adolf Zeising in the nineteenth century, and to theorist Matila Ghyka and the practitioners Ernst Neufert and Le Corbusier in the twentieth. In the latter's writings and designs the Golden Section seems to play the role of a scholarly element which shows the master's theoretical erudition, leading to contemporary architects such as Ricardo Bofill.
Introduction: Vitruvius
Proportion is the first and principal subject of architectural theory. What we know about the writings of ancient Greek architects is minimal, but there is evidence that they gave an account of the proportions of their temples [Wesenberg 1983].[1] This would indicate a reflected, developed way of design. Taking the next step the architect does not think only about the 'how' but also the 'why'. This stage is documented by the De architectura libri decem (c. 33 –22 B.C.), the oldest preserved architectural treatise of antiquity and surely the most comprehensive. Vitruvius offers not only practical advice about designing, building types, forms, techniques, but also theoretical thoughts about tasks, origins, and — at least partially — the aesthetics of architecture. In both aspects De architectura becomes the basis for subsequent treatises on architecture. So this is where we should start in order to consider the role of the Golden Section in architectural theory.
For Vitruvius the educated architect has to know arithmetic and geometry (I,1,4). Thus his own rules of design combine both methods: all plans of temples are completely developed by geometrical partitions and relations (IV,4,1; IV,7), with the round temple even the elevation (IV,8,1–3). Arithmetic modular operations using the lower diameter of the column as the base module regulate the dimensions and proportions of the columns and intercolumniations (IV,1). Here Vitruvius uses geometrical methods too — the height of the entablature and its decoration (III,8–12) and the tapering of the shafts (III,3,12) are bound to the columns' dimensions. Even the modulus is derived from a division of the temple's width, dependent on each temple-type (III,3,7; IV,3,3–4; IV,3,7).
This interrelationship of modularity and geometry is also found in the detailed analysis of the proportions of the human body (III,1). Vitruvius presents his canon, the famous figure of a man in circle and square, in support of his claim that "no Temple can have a rational composition without symmetry and proportion, that is, if it has not an exact calculation of members like a well-shaped man" (III,1,1). [2] So the body is a model by virtue of its perfection of symmetrical shaping first and foremost and not in its inherent proportions, which is often misunderstood; cf. Frings [1998]. The human body, as an example of modular creation from nature, is chosen by Vitruvius as a paradigm for the required rules of proportion.
The Roman architect and author is far away from the development of a convincing system of proportions. However, his precepts of design are a notable attempt to unify different methods apparently drawn from the Greek and Roman traditions. His knowledge of musical theory seems to exceed his skills in geometry, in which he takes less interest. The only sophisticated geometry is ad quadratum, which organizes the capital of the Corinthian order (IV,1,11). We do not find the Golden Section in the De architectura libri decem, which gave frame and subject matter to subsequent architectural theory.
In the Middle Ages architectural writing may be categorized according to the source: by scholars in encyclopedias referring to Latin authors like Vitruvius or Pliny, by theologians who explain the building of the church (ecclesia materialis) in allegoric ways, pointing to the ecclesia spiritualis, and lastly by the practitioners of architecture themselves. In this third category we have some books of simple advice (e.g., the mappa claviculae, 8th century [Mortet 1911: 225-267]) and of patterns and building designs (e.g., Villard d’Honnecourt, ca. 1220/25–1230/35 [Hahnloser 1972]). In all three categories the Golden Section is lacking.
The Renaissance: Pacioli and Silence
The architectural theories of the Early Renaissance frequently use the human model as a paradigm of good architecture, though in quite different ways. Leon Battista Alberti addresses scholars in his architectural treatise De re aedificatoria, completed c. 1450, his complex aesthetics proclaiming the laws of numerus, finitio and collocatio, in order to achieve the ultimate goal, concinnitas. Alberti recommends simple numerical proportions to the architects, especially musical ones; ch. 9,5 [Alberti 1967: v. 2, 822–824]. In Alberti’s De pictura, Filarete (c. 1461–64) reads the Homo mensura-sentence of Protagoras and takes it literally, so that he derives buildings as far as possible from the human body. Since Filarete, in his Trattato di architettura (ch. 8), only partially succeeded — in the anthropomorphic column — he does not by far surpass Vitruvius. An anthropomorphic architecture, which could even be called anthropomimetic[3], is designed by Francesco di Giorgio Martini from Siena in his two architectural treatises (ca. 1465–1492; Trattati di Architettura [Martini 1967], and Das Skizzenbuch [Martini 1989]). He also knows to realize this close parallel to the human body for the ground plan and even for façade and entablature of a church, always in order to give the building the quality of beauty. Like Vitruvius, Francesco combines geometrical operations like the square root with a modular approach. Neither in the two versions of his architectural treatise nor in his opinion about Milan cathedral does Francesco speak of the Golden Section, nor does Alberti, nor Filarete. Neither do the studies of Vitruvius in the Cinquecento, e.g., Guillaume Philandrier [1544] or Daniele Barbaro [1556], mention the Golden Section. As Vitruvius did not use it, it presumably did not occur to the architectural theorists of the Renaissance to search for it in Euclid’s Elements.
Luca Pacioli, however, was a great admirer of the Golden Section, as evidenced by the name of his treatise, Divina proportione, which actually comprises three independent works [Pacioli 1509]. At the beginning Pacioli places the Compendium de divina proportione, the book about the Golden Section, which Pacioli dedicated in December 1498 to Duke Lodovico Sforza of Milan.[4] The learned Franciscan Pacioli finds five attributes of God in this special proportion, the first four of which are unity and uniqueness, trinity, the impossibility of defining in terms of human ratio, and the immutability. In the fifth, functional comparison Pacioli sets the "divine proportion" in relation to the Platonic quintessence:
"Si commo Idio l’essere conferesci alla virtu celeste per altro nome detta quinta essentia e medinante quella ali altri quatro corpi semplici cioe ali quattro elementi Terra... E per questi l’essere a cadaun altra cosa in natura. Cosi questa nostra proportione l’essere formale da (secondo ... Timeo) a epso cielo atribuendoli la figura del corpo detto Duodecedron, altramente corpo de 12 pentagoni." (As God confers being to the celestial virtue, called by the other name 'fifth essence', and through that one to the other foursimple bodies, that is, to the four earthly elements...and so through these to every other thing in nature. Thus this our proportion is the formal being of (according to Timaeus) heaven, attributing to it the figure of the solid called Duodecahedron, otherwise known as the solid of twelve pentagons) [Pacioli 1509, ch. I, 5, f 3v-4r]. Here we clearly recognize Pacioli's metaphysical character, Platonic and Christian.
In the rest of the first book, Pacioli describes in detail the geometrical attributes of the "proportion having a middle and two extreme ends", in medieval words used also by Pacioli. He does not advance the field of research in his discipline, does not give any advice or thought about the practical application in the pictorial arts. In fact Pacioli’s achievement consists more in diligent compilation than in scientific originality.[5] Harsh critique has also been uttered, since Pacioli declares much but proves nothing.[6]
Of course the Compendium is not architectural theory, but Pacioli himself wrote probably by c.1509 in Venice a small Tractato de l’architectura, published in the Divina porportione as the second book.[7] He states that he has written this small work — only 22 leaves — at the request of some "respectable masons, most diligent friends of sculpture and achitecture", named personally as his disciples. He promises them "norms and methods of arriving at the desired effect in architecture".[8] His connection with architecture dates from his time in Rome, when he was Alberti's guest for months.[9] Later in Urbino between 1472 and 1474, he had occasion to meet Francesco di Giorgio Martini and Bramante, and in Milan (1494–1499/1500) he collaborated with Leonardo.
What he offers would scarcely have satisfied the architects — his Tractato de l’architectura is a conventional compilation of the orders following Vitruvius, almost without any critique or changes, often paraphrasing the Roman authority in Latin. For Pacioli, too, the human body serves as example for perfect proportions, but also in the orders as a concrete model. Here Pacioli achieves his own meaning, when he sees the Ionic column, because of the pendent volutes, as "melancholic and deplorable, widow-like", whereas the Corinthian column is "juvenile, fine, serene and … more graceful".[10]
Pacioli understands the Vitruvian figure of the man in circle and square with Filarete in the sense that the geometrical figures have their origin in the human body (ch. I,1, f. 25r). He is the first who describes the so-called homo vitruvianus with spread legs, so that it must be expanded violently to fit in the square, like Cesariano illustrates it later. A third geometrical form is added by Pacioli, the equilateral triangle, drawn in a profile of a head with irregular grid (ch. I,1, f. 25v). A variant of this figure introduces the illustrations at the end of the book, with only some gridlines lacking (Figure 1).
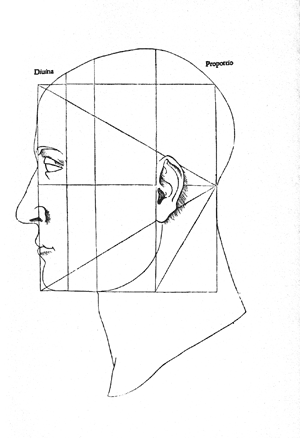 With
this he again intellectually follows Filarete [1972: I, 18], who already
understood the head as the most noble part of the body and thus as the origin of the
system of measurements. Concerning the drawing he is nearer to Francesco di Giorgio's
illustration of the head in the entablature, or to the medieval tradition of
pattern-books, which use the equilateral triangle as means to draw a profiled head,
e.g. Villard d'Honnecourt [Hahnloser 1935: f. 18v, pl. 36e].[11] So
Pacioli puts at the beginning of his treatise the three principal forms
circle, square, and triangle — similar to Euclid in the Elements.
With
this he again intellectually follows Filarete [1972: I, 18], who already
understood the head as the most noble part of the body and thus as the origin of the
system of measurements. Concerning the drawing he is nearer to Francesco di Giorgio's
illustration of the head in the entablature, or to the medieval tradition of
pattern-books, which use the equilateral triangle as means to draw a profiled head,
e.g. Villard d'Honnecourt [Hahnloser 1935: f. 18v, pl. 36e].[11] So
Pacioli puts at the beginning of his treatise the three principal forms
circle, square, and triangle — similar to Euclid in the Elements.
This shows the eminent role Pacioli gives to geometry. In fact, he harshly criticizes the architects who make use of geometry — like other craftsmen, too — "although they don't know it". They do not even know of the world’s order in measure, number and weight, so that often their buildings fall down.[12]
In this chapter he recommends a special three-dimensional form often used in architecture, the body with 72 planes, which he treats also in the Compendium de la divina proportione (Figure 2; cf. Divina porportio I,54, f. 16rv). His description and the example Pantheon lead to the conclusion that he thinks of a coffered cupola, but perhaps of complex cupola-like Gothic vaults too.[13] Despite this stress on geometry, Pacioli’s approach to proportion remains conventional and Vitruvian.
 Another
chapter of his architectural treatise recommends the Platonic regular bodies
in its title.[14] So
buildings were "not to criticize", he writes in this chapter,
if for details like bases or capitals here and there were used these mathematic
bodies, although Vitruvius did not mention them at all. They not only "adorn
buildings, but also give the scholars and wise opportunity to speculate,
in so far as they are always constructed by that sacred and divine proportion",
which we call the Golden Section.[15] Then
he tells the anecdote of Phidias who gave a statue of Ceres in Rome an icosahedron
for the element of water, earning highest praise.
Another
chapter of his architectural treatise recommends the Platonic regular bodies
in its title.[14] So
buildings were "not to criticize", he writes in this chapter,
if for details like bases or capitals here and there were used these mathematic
bodies, although Vitruvius did not mention them at all. They not only "adorn
buildings, but also give the scholars and wise opportunity to speculate,
in so far as they are always constructed by that sacred and divine proportion",
which we call the Golden Section.[15] Then
he tells the anecdote of Phidias who gave a statue of Ceres in Rome an icosahedron
for the element of water, earning highest praise.
Hence it seems to be clear that Pacioli does not recommend at all to replace traditional parts, whose "correct" formation has been the architects' and sculptors' task for decades, by the Platonic polyhedra. Pacioli himself describes the orders in detail, as already stated, in Vitruvian manner. On the contrary he thinks of a selected insertion as the case may be, like we know it from other examples in the history of architecture (for instance Vitruvius' explanation of caryatids; De architectura I,1,5–6), which attest to the architect’s historical knowledge. There is no general recommendation of the Golden Section for use in architecture, and it is only implicit in the Platonic solids.
On the contrary Pacioli recommends to architects — besides the Vitruvian rules — the forms of circle and square, whereas the formerly praised triangle is lacking. He also recommends simple ratios of integral numbers like 1/2, 1/3, 3/4, 2/3 etc. If irrational proportions like those based on √2 must be used, the architects should draw them separately and not calculate them.[16] So Pacioli advises the practitioners on commensurable proportions, which are easy to construct on drawing board or building site — he apparently thinks of practicability and is aware of the limited mathematical skills of his readers. In this context the Golden Section does not play any role.
The three illustrations at the end of Pacioli's text only explain the technical terms of some parts of the building (column and pedestal, entablature) and present — without relation to the text — an ideal architecture, the façade of Salomon’s temple. The second version of the profiled head is titled Divina Proportio, establishing a connection between the mathematical tract and the architectural treatise (Figure 1). None of the lines show the Golden Section; on the contrary they are simply remains of the irregular grids of the former version.
Neither in the text nor in the illustrations is the Golden Ratio recommended for practical use. This is astonishing, given the great valuation as divina proportione, but has its reasons: Pacioli does not want to give concrete proportional precepts but to show the meaning of calculated proportions in architecture in general, similar to Vitruvius. Pacioli’s role in architectural theory has been overestimated for a long time.[17] He presents himself as mathematician, who certainly deals with Vitruvius, but who does not develop his own propositions on how to design a building.
 In
stark constrast, this is exactly the achievement of Sebastiano Serlio (1475–1554).
He dedicates the first volume of his great architectural treatise to the
orders [Serlio 1537]. His consistent system of the five orders with simple
proportional construction is the lesson book the practitioners had been
waiting for. With a juxtaposition of Italian text and instructive figures,
Serlio advisedly addresses the builders. With this treatise he becomes
the creator of the modern orders.
In
stark constrast, this is exactly the achievement of Sebastiano Serlio (1475–1554).
He dedicates the first volume of his great architectural treatise to the
orders [Serlio 1537]. His consistent system of the five orders with simple
proportional construction is the lesson book the practitioners had been
waiting for. With a juxtaposition of Italian text and instructive figures,
Serlio advisedly addresses the builders. With this treatise he becomes
the creator of the modern orders.
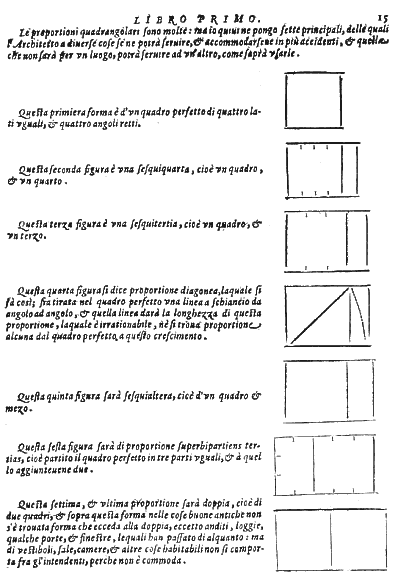
Following the same traditions as had Pacioli, Serlio uses simple, commensurable proportions. The columns are constructed in a module system, the entablature and its parts use divisions of the module, and also the pedestal is designed by geometrical operations. The dado is an ashlar, which is slendered from Tuscan to Composite order — in the Tuscan order it is a cube, in the Doric order its height is equal to the square root of its width, in the Ionic one and a half its width, in the Corinthian one and two thirds, and in the Composite at last the cube is doubled.[18] These are some of the seven most important proportions which Serlio [1545: 21r] later mentions with their classical terms (Figure 3). Here, too, and even in the construction of the regular pentagon shortly before (f. 20v) the Golden Section is absent, although this would be the right place. The entire book about geometry is silent on the Golden Ratio — indeed, in the entire work of Serlio, it is lacking.
This surely cannot be explained only by Serlio’s pragmatic attitude. There is no need for such a complicated proportion. The same is true for the other great treatises from Vignola and Palladio, Scamozzi and the Italian classicists to the theory of the 19th century. Nowhere occurs the Golden Ratio; in the overwhelming majority of these treatises, the simple, commensurable ratios are recommended, and the only irrational proportion is the well-known √2. n addition to the human body as relative figuration, Venetian authors of the Cinquecento (e.g., Francesco Giorgi, Barbaro) introduce musical harmonies. When Palladio deals with the heights of rooms, the Golden Ratio could have been employed, but Palladio sets the length, width, and height using other mathematical relations [Palladio 1570: ch. I, 23].
Let us look at two persons at the edge of architectural theory, who were active as artists and theorists of proportions. Even a master of the applied perspective such as Leonardo, Pacioli’s collaborator, did not take interest in the Golden Ratio but gives only approximations to the regular pentagon.[19] Albrecht Dürer indeed knew — perhaps by Pacioli himself on the second journey to Italy 1506/7 — a correct construction of the regular pentagon by means of the Golden Section, but he did not seem to make up his mind about their connection [Dürer 1525: II,15]. His practical instrument called "Vergleicher" (comparer), which should help to construct perspective human figures, produces a continuous proportion, not to be confused with the Golden Ratio.[20] We see an image similar to Pacioli: in the geometrical writings Dürer, too, describes the construction of the pentagon and knows the Golden Section, but in his tract on architecture, neither occur [Dürer 1527].
The Nineteenth Century: Zeising
In fact, it is not before the middle of the 19th century that the Golden Section enters architectural theory. In the time of the beginning of Historicism and of the great scientific discoveries and theories, Adolf Zeising (1810–76) began his researches on proportions in nature and art. Coming from the philosophical aesthetics, he is not literally an architectural theorist. His work inaugurates that kind of literature on art that tries to analyze the proportions in order to gain information about the procedure of design. Unfortunately, in the early stages of this literary movement, there is a considerable lack of methodical reflection and historical anchorage.
Zeising's work is largely unresearched, his sources and inspirations, his writings and their impact.[21] After having retired from active service as a secondary-school professor in 1853, he devoted himself to his studies and lyrics. Even the first of Zeising's publications [Zeising 1854] declares in its title his program: New Theory of the proportions of the human body, developed from a basic morphological law which stayed hitherto unknown, and which permeates the whole nature and art, accompanied by a complete summary of the prevailing systems.[22] This is an unprecedented claim — to have detected the one morphological law in the formations of art and nature, and it marked the beginning of an entirely different approach in the literature.
Having extensively discussed actual theories Zeising develops his own aesthetics, born from a romantic, idealistic tradition. In this theory the Golden Section plays an important role as the perfect balance between absolute unity and absolute variety. Zeising is convinced that in the Golden Section "is contained the fundamental principle of all formation striving to beauty and totality in the realm of nature and in the field of the pictorial arts, and that it from the very first beginning was the highest aim and ideal of all figurations and formal relations, whether cosmic or individualizing, organic or inorganic, acoustic or optical, which had found its most perfect realization however only in the human figure" [Zeising 1854: V].
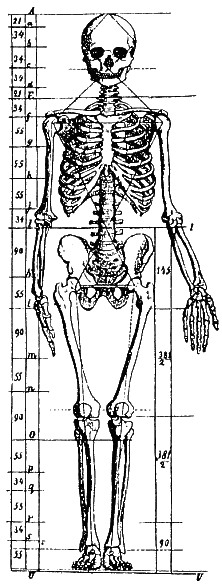 Thereto
he presents his own proportional analyses of the human body, comprising
vertical and horizontal measures, but illustrates it separately (Figure
4). He deals in a loose manner with numbers, only using the lower numbers
of the Fibonacci series as approximations, replacing the 89 by 90. After
the analysis of the ideal man he examines antique statues and explains
the differences between sexes, races and stages of life from embryo to
old man, then he turns to nature: stars, crystals, plants and animals.
Agreeing with the old idea of natura naturans, Zeising declares
that man has to "continue nature" in his creations by means of
the Golden Section.[23]
Thereto
he presents his own proportional analyses of the human body, comprising
vertical and horizontal measures, but illustrates it separately (Figure
4). He deals in a loose manner with numbers, only using the lower numbers
of the Fibonacci series as approximations, replacing the 89 by 90. After
the analysis of the ideal man he examines antique statues and explains
the differences between sexes, races and stages of life from embryo to
old man, then he turns to nature: stars, crystals, plants and animals.
Agreeing with the old idea of natura naturans, Zeising declares
that man has to "continue nature" in his creations by means of
the Golden Section.[23]
Less intensively he looks at works of art, at the Parthenon — he is the first to publish an analysis finding in it the Golden Section, at two important churches in Germany (Cologne cathedral, St. Elizabeth in Marburg/Hesse), and from painting he chooses the Sistine Madonna of Raphael. To find the Golden Section in music gives him trouble, but he embraces poetry, philosophy and religion. In an appendix he gives artists practical advice on the construction of the human figure and on the measuring of proportions.
Only some years before Zeising published his New Theory, the term "Goldener Schnitt" was created. It can first be read in lesson-books on geometry and mathematics in the 1830s [Wolff 1833: 127; Ohm 1835: 194, n. on Prop. 5; and Kroll 1839: sec. 178, p. 189]. In 1849 a small book about the special properties of the Golden Section from a mathematical-geometrical point of view came out [Wiegand 1849]. In the same year the long tradition of proportional analyses of the human body was continued by a new work, cited by Zeising.[24] We have to see Zeising in this tradition; here is his home.
One should not underestimate Zeising’s impact. It is he who introduces the Golden Section into the literature on art and so placed it at the artists' disposal. From the above historical discussion we can conclude that Zeising 'discovered' the Golden Section for architecture and the pictorial arts in general.[25] In a strange combination of idealistic aesthetics and pretended exact-scientific analysis, he proclaims a simple truth about the rather complex manifestations of nature and about the scarcely less divergent forms of art, which in this time did not show a stylistic unity. In an age of deep uncertainty Zeising returns to an anthropocentric, normative aesthetics, which seemed to have become out of favor since the French Rationalism and British Empirism of the 18th century. He rehabilitates the man as the crown of creation in the actual Darwin debate, and he rehabilitates the concept of the inherent harmony of the cosmos, which he sees as intelligible and in keeping with the artistic production of mankind.
It is probably this unity that caused the immense popularity of Zeising’s convincingly formulated theory. Numerous “disciples” adopted his axiom and widened the scope to other arts and further parts of nature.[26] Of all attempts to find norming proportional systems in the history of art (e.g. ad quadratum, ad triangulum, the "similar figures" of August Thiersch), those devoted to the Golden Section are surely the most numerous and till now the most pervasive.[27] Although these universal morphologies can be considered within the tradition of rational positivism, many metaphysical studies have come out since the beginning of the 20th century (e.g., [Ghyka 1927]), a tradition that continues with the modern 'esoterics' (e.g., [Bühler 1996]).
The arising psychology tried to prove the effect of the Golden Section on people, which had become the paradigm of experimental psychology. Gustav Theodor Fechner in 1864 observed that in a series of rectangles between square and double-square, his probationers preferred the Golden Ratio rectangle.[28] Since he could not confirm this result with ellipses or in the simple division of lines he said that "Zeising thought too highly of the aesthetic value of the Golden Section" [Fechner 1865: 162], which Fechner [1913] then even ridicules. After the Einfühlungspsychologie, established by Theodor Lipps, had called into question the absolute meaning of the Golden Ratio, and numerous varying experiments could not even reproduce Fechner’s results for the "golden rectangle", nowadays it is no longer controversial that it is impossible to establish a psycho-physical canon of forms. Nevertheless Fechner's experiments had a considerable effect on the comprehensive systems of the scientific aesthetics since the beginning of the 20th century; e.g., Frankl [1938: 43] sees the Golden Section as a constituting element of his "harmonial style".[29]
The Twentieth Century: Neufert and Le Corbusier
From more or less scientific analyses of proportions, art-historical science, and psychology in the first decades of the 20th century, a general conviction arose that all artistic activity is based on fundamental "arch-proportions". The established scientific art history only incidentally participates in those speculations, but also formulates little contradiction.[30] Some groups of artists seem to have discussed problems of proportions relating to the Golden Ratio — we know that Paul Serusier used it as instrument to control his designs [Herz-Fischler 1997], but the Parisian group of cubists Section d’or, with Delaunay, Duchamp, Léger and Gris, conceived its name rather as a signet for their interest in science and philosophy. Other architects of the time were strongly interested in proportions; e.g., the Dutchman Johannes Ludovicus Mattheus Lauweriks developed his own system, and Peter Behrens experimented in this field as well.
Within this context the Golden Section attracted two architects whose attitude to Proportions could not be more different: Ernst Neufert and Le Corbusier. More efficacious for architecture probably was Neufert’s decision to embrace the Golden Section in his famous Bauentwurfslehre from 1936, coming out to this day in endless editions and translations. Neufert (1900–1986), a disciple and employee of Walter Gropius, combines rational norming with an aesthetic impetus. He propagates the Golden Ratio as this architectural principle of proportion, that together with his own normed measures leads to a "spiritual permeation" and a renewal of architectural formation by "an inner law" in the spirit of Antique, Gothic, Renaissance, and Classicism of Palladio and Schinkel [Neufert 1936: 30].[31] In fact Neufert does not really join Zeising’s human "golden" proportions and his own anthropometric normed measures, because he chooses distances very pragmatically by looking at interior architecture (Figure 5, Figure 6) [Neufert 1936: 23, 24].
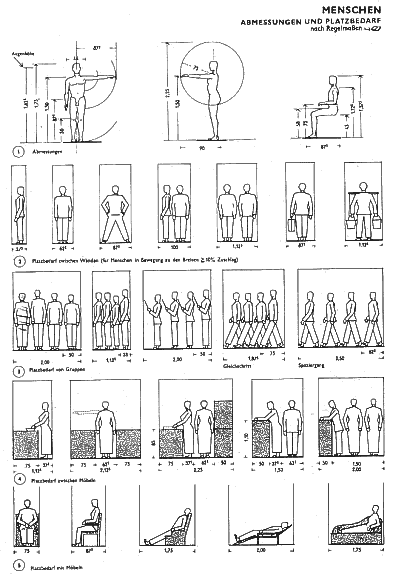 Neufert
explains historical systems of proportion and the Golden Mean more extensively
in his Bauordnungslehre from 1943. Again the Golden Section provides
the primary link between all harmonies in architecture. But now Neufert
ends
his historical overview with an open statement, pointing to a verse of
Goethe about the fathers' heritage and the appeal to shape the modern
structures liberally based on this inner fullness [Neufert 1943: 54]. Above
all, the Bauordnungslehre spreads the knowledge of different proportional
systems, and particularly of the Golden Section, among students of architecture.
Even if Neufert desires aesthetic consequences of his norms, he had caused
exactly the contrary — a planning in dimensions caused by function
and techniques of production.
Neufert
explains historical systems of proportion and the Golden Mean more extensively
in his Bauordnungslehre from 1943. Again the Golden Section provides
the primary link between all harmonies in architecture. But now Neufert
ends
his historical overview with an open statement, pointing to a verse of
Goethe about the fathers' heritage and the appeal to shape the modern
structures liberally based on this inner fullness [Neufert 1943: 54]. Above
all, the Bauordnungslehre spreads the knowledge of different proportional
systems, and particularly of the Golden Section, among students of architecture.
Even if Neufert desires aesthetic consequences of his norms, he had caused
exactly the contrary — a planning in dimensions caused by function
and techniques of production.
On the other hand we see planning in proportions caused by aesthetic reasons in the other great system of the 20th century, Le Corbusier's (1887–1965) Modulor. He works up to this later treatise with different proportional systems in his early years — employment at Behrens and study of Lauweriks' designs — in the manifesto Vers une architecture. Written in a prophetic tone like all of his books, it already presents the Golden Section as natural rhythm, inborn to every human organism [Le Corbusier 1923: 65]; cf. [Brooks 1997]. However Le Corbusier does not yet recommend concrete proportions, but only to use "tracés regulateurs", measure-ruler, to control the geometrical organisation of design, always façades in his examples. The geometrical figures of the measure-ruler themselves are at the architect's liking, but Le Corbusier presents only a few, and his examples strongly resemble those in Auguste Choisy's history of architecture, who also delivers Le Corbusier's figures [1923: 67–70]; cf. [Choisy 1899].[32]
 Only
in his most important tract, Le Modulor (1948), Le Corbusier mentions his
model, when he tells a story of discovery with postcards in his small Paris
apartment, which he states should have happened in 1909. Then he narrates
the development of his own system of measures, the Modulor, beginning with
an order by the office for standardization in Vichy-France (AFNor) in 1943.
Till then he seemed to have organised designs for façades and paintings
in a spontaneous and unsystematic manner by means of tracés regulateurs and Golden Mean, although post
festum perhaps; cf. the examples in [Le
Corbusier 1948: 34 ff., 213–16]. Possibly only then, through Neufert's
Bauordnungslehre, did Le Corbusier receive the inspiration to systematize
and organize consequently his tracés regulateurs idea [Hilpert 1999].
Only
in his most important tract, Le Modulor (1948), Le Corbusier mentions his
model, when he tells a story of discovery with postcards in his small Paris
apartment, which he states should have happened in 1909. Then he narrates
the development of his own system of measures, the Modulor, beginning with
an order by the office for standardization in Vichy-France (AFNor) in 1943.
Till then he seemed to have organised designs for façades and paintings
in a spontaneous and unsystematic manner by means of tracés regulateurs and Golden Mean, although post
festum perhaps; cf. the examples in [Le
Corbusier 1948: 34 ff., 213–16]. Possibly only then, through Neufert's
Bauordnungslehre, did Le Corbusier receive the inspiration to systematize
and organize consequently his tracés regulateurs idea [Hilpert 1999].
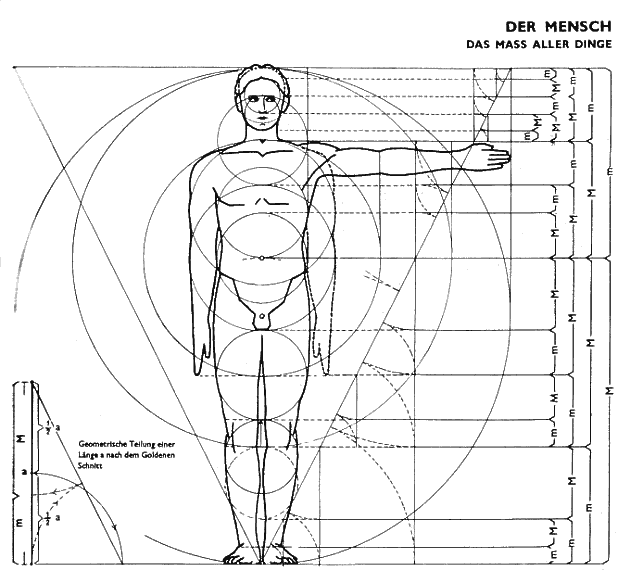
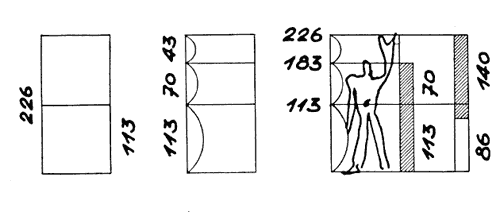
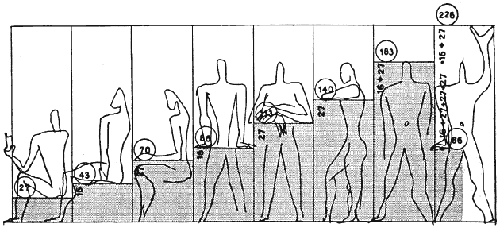 The
Modulor in Le Corbusier’s story combines square and Golden Section,
but as a result it does not offer anything else than a modular system.
From a blue series of numbers (Golden Section of the total height) and
a red series (height of the navel) results a sequence of measures from
27 cm to 226 cm (and then much more) in steps of 27 and 16 (Figure 7, Figure
8). In the role of the navel as origin of the red series, Le Corbusier
alludes to the tradition of the homo vitruvianus and the related speculations
about the harmonies in the anthropocentric cosmos, well shown in a summing
figure in the second book Modulor 2 [Le Corbusier 1955: fig. 15] (Figure
9).
The
Modulor in Le Corbusier’s story combines square and Golden Section,
but as a result it does not offer anything else than a modular system.
From a blue series of numbers (Golden Section of the total height) and
a red series (height of the navel) results a sequence of measures from
27 cm to 226 cm (and then much more) in steps of 27 and 16 (Figure 7, Figure
8). In the role of the navel as origin of the red series, Le Corbusier
alludes to the tradition of the homo vitruvianus and the related speculations
about the harmonies in the anthropocentric cosmos, well shown in a summing
figure in the second book Modulor 2 [Le Corbusier 1955: fig. 15] (Figure
9).
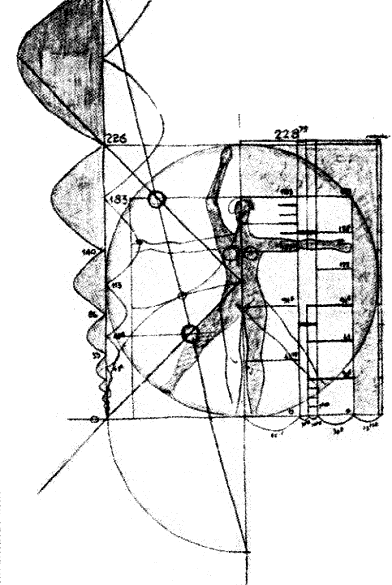 The
Modulor has some deficiencies, however. First, although Le Corbusier meant
for it to be used for all dimensions, vertical and horizontal, he bases
it solely on the vertical dimension. Further it is based on approximations
to the Fibonacci numbers. Since the blue and the red series can be combined,
the system becomes so elastic that the Golden Section is hard to detect.
Neufert himself criticizes, in a newer edition of the Bauordnungslehre,
both the loose practice of rounding off numbers, so that some additions
are no longer correct, and further inaccuracies when transcribing the
metrical measures into the British system of inches. Finally the Modulor
is indeed
not far from Neufert's own "Oktameter-System" [Neufert
1941]. Therefore the Modulor should not be called a system of proportions
but a catalogue of irregular measures.
The
Modulor has some deficiencies, however. First, although Le Corbusier meant
for it to be used for all dimensions, vertical and horizontal, he bases
it solely on the vertical dimension. Further it is based on approximations
to the Fibonacci numbers. Since the blue and the red series can be combined,
the system becomes so elastic that the Golden Section is hard to detect.
Neufert himself criticizes, in a newer edition of the Bauordnungslehre,
both the loose practice of rounding off numbers, so that some additions
are no longer correct, and further inaccuracies when transcribing the
metrical measures into the British system of inches. Finally the Modulor
is indeed
not far from Neufert's own "Oktameter-System" [Neufert
1941]. Therefore the Modulor should not be called a system of proportions
but a catalogue of irregular measures.
It is not our task to examine where Le Corbusier has built the Golden Section and the Modulor. So it should do for our purpose to say that he applies his system less than thoroughly. Le Corbusier's use of the Golden Section begins by 1927 at the Villa Stein in Garches, whose rectangular proportion in ground plan and elevation, as also the inner structure of the ground plan, approximately show the Golden Section [Le Corbusier 1948: 34 ff.].[33] Le Corbusier himself calls his Unité d’Habitation in Marseille (1945–52) a demonstration of his Modulor system. Indeed the real measures considerably differ from the theory: real length 140 m, instead of Modulor 139,01 m; width 24 m, Modulor 25,07 m; height 56 m, Modulor 53,10 m [Le Corbusier 1948: 134, cf. the series of measures p. 84]. To address these differences, attempts have been made to trace back the building’s dimensions not to the Modulor but to the exact relations of the Golden Mean, but with little success [Padovan 1999: 332 ff.].
Le Corbusier's importance and his great impact seem to originate in his normative aesthetics, which propagates the combination of abstract geometry and anthropomorphic measures. So nearly all modern architectural lesson books extensively describe the Golden Section, e.g., Ching [1996] or Krier [1988]. Here and there it serves as a theoretical reflection that can be given — post festum? — to architectural designs [Bofill 1985].
Conclusion
For a long time the Golden Section does not occur in architectural theory. It first appears in the 19th century, through Zeising and Fechner, and then rises to a certain fashion in the third and fourth decade of the 20th century, from which Neufert and Le Corbusier get to know it. Neufert held out great hopes for a renewal of architecture through the Golden Mean, but he soon became sober. Nevertheless he presents it in extenso. After early experiments Le Corbusier uses the Golden Section to develop his catalogue of measures, which has — due to roundings and combinations — not much in common either with the Golden Mean or with the Fibonacci series. In fact, Neufert and Le Corbusier seem to use the Golden Section as a way to embellish their own subjective artistic creation by theory and ratio. In any case, the Golden Section certainly does play a role in the writings of these architectural theorists. Prior to the 19th century, however, the Golden Section is simply absent in written architectural theory.
References
Alberti, Leon Battista. 1967. De re aedificatoria. Testo latino e traduzione a cura di Giovanni Orlandi. Introduzione e note di Paolo Portoghesi, 2 vols. Milan: Edizione Il Polifilo (Trattati di Architettura, 1).
Barbaro, Daniele. 1556. I dieci libri dell'architettura di M. Vitruuio tradutti e commentati da Monsignor Barbaro eletto Patriarca d'Aquileggia. Venice: Francesco Marcolini.
Bochenek, Johannes. 1875. Die männliche und weibliche Normalgestalt nach einem neuen System, Berlin.
Bofill, Ricardo. 1985. Taller de Arquitectura. Yukio Futagawa, ed. New York: Rizzoli.
Borissavlievitch, Miloutine. 1954. Traité d’esthétique scientifique de l’architecture. Paris: Blanchard.
Brooks, H. Allen. 1997. Le Corbusier's formative years: Charles-Edouard Jeanneret in La Chaux-de-Fonds. Chicago: University of Chicago Press.
Bühler, Walther. 1996. Das Pentagramm und der Goldene Schnitt als Schöpfungsprinzip. Stuttgart: Verlag Freies Geistesleben.
Carus, Carl Gustav. 1853. Symbolik der menschlichen Gestalt: Ein Handbuch zur Menschenkenntnis. Leipzig: Brockhaus.
Ching, Francis D. K. 1996. Architecture: form, space and order. New York: van Nostrand Reinhold (first ed. 1979).
Choisy, Auguste A. 1899. Histoire de l’architecture, 2 vols. Paris: Gauthier-Villars.
Cook, Theodore A. 1922. A new disease in architecture. In: The Nineteenth Century and after, vol. 91, p. 521–532.
Daly Davis, Margaret. 1977. Piero della Francesca's Mathematical Treatises: The trattato d'abaco and Libellus de quinque corporibus regularibus. Ravenna: Longo.
Dessoir, Max. 1906. Ästhetik und allgemeine Kunstwissenschaft. Stuttgart: Enke.
Doczi, György. 1996. The Power of Limits: Proportional Harmonies in Nature, Art and Architecture. Boston MA: Shambhala.
Dürer, Albrecht. 1525. Underweysung der messung. Nuremberg. Rpt. 1972. Unterschneidheim: Verlag Dr. Alfons Uhl.
Dürer, Albrecht. 1527. Etliche underricht zu befestigung der Stett Schlosz und flecken. Nuremberg. Rpt. 1969. Unterschneidheim: Verlag Walter Uhl.
Dürer,
Albrecht. 1956/1966/1969: see Rupprich, Bernhard. Fechner,
Gustav Theodor. 1865. Über die Frage des goldnen Schnitts.
In: Archiv für die zeichnenden Künste
vol. 11, p. 100–112. Fechner,
Gustav Theodor. 1876. Vorschule der Ästhetik. Leipzig:
Breitkopf & Härtel. Fechner,
Gustav Theodor. 1913. Warum wird die Wurst schief durchgeschnitten? In: id.
Kleine Schriften, Leipzig: Breitkopf & Härtel, p. 255–270. Filarete (Antonio Averlino). 1972. Trattato di Architettura.
Testo a cura di Anna Maria Finoli e Liliana Grassi. Introduzione e note di Liliana Grassi,
2 vols. Milan: Edizioni Il Polifilo (Trattati di Architettura, 2). Filarete (Antonio Averlino). 1965. Filarete's Treatise on
Architecture, being the Treatise by Antonio di Pietro Averlino, known as Filarete,
translated with an introduction and notes by John R. Spencer, 2 vols. New Haven, London:
Yale University Press (Yale Publications in the History of Art, 16).
Francesco di Giorgio Martini. 1967. Trattati di Architettura,
Ingegneria e Arte militare. Testo a cura di Corrado Maltese. Trascrizione di Liliana
Maltese Degrassi, 2 vols. Milan: Edizioni Il Polifilo (Trattati di Architettura, 3). Francesco di Giorgio Martini. 1989. Das Skizzenbuch des Franceso
di Giorgio Martini (Codicetto/taccuino Vaticano). Vat. Urb. lat. 1757. Facsimile with
introducing volume by Luigi Michelini Tocci. Zurich: Belser (Codices e Vaticanis selecti quam
simillime expressi iussu Ioannis Pauli PP II consilio et opera curatorum Bibliothecae Vaticanae,
vol. 80). Frankl, Paul. 1938. Das System der Kunstwissenschaft.
Brünn, Leipzig: Rohrer. Fredel, Jürgen. 1992. Dürer und der Goldene Schnitt. In:
Ilsebill Barta Fliedl and Christian Geissmar, ed. Die Beredsamkeit des Leibes: Zur
Körpersprache in der Kunst. Salzburg, p.
174–180. Fredel, Jürgen. 1998. Maßästhetik: Studien zu
Proportionsfragen und zum Goldenen Schnitt. Hamburg: LIT Verlag. Frings, Marcus. 1998. Mensch und Maß: Anthropomorphe Elemente
in der Architekturtheorie des Quattrocento. Weimar: vdg Verlag und Datenbank für
Geisteswissenschaften. Funck-Hellet, Charles. 1951. De la Proportion:
L’équerre des maîtres d’oeuvre. Paris: Éditions Vincent,
Fréal & Cie. Goeringer, Adalbert. 1893. Der goldene Schnitt (göttliche
Proportion) und seine Beziehungen zum menschlichen Körper, zur Gestalt der Tiere, der
Pflanzen und Krystalle, zur Kunst und Architektur, zum Kunstgewerbe, zur Harmonie der Töne
und Farben, zum Versmass und zur Sprachbildung. Munich: Lindauer. Gros, Pierre, ed. 1990. Vitruve, De l'architecture, livre III,
texte établi, traduit et commenté par Pierre Gros, Paris: Les Belles Lettres
(Collection des Universités de France, publiée sous le patronage de l'Association
Guillaume Budé). Ghyka, Matila C. 1998. Esthétique des proportions dans la nature
et dans les arts, Paris: Éditions du Rocher (first ed. 1927). Hahnloser, Hans R., ed. 1935. Villard de Honnecourt: Kritische
Gesamtausgabe des Bauhüttenbuches ms. fr 19093 der Pariser Nationalbibliothek. Vienna:
Schroll. Hambidge, Jay. 1920. Dynamic Symmetry: The Greek Vase. New Haven:
Yale University Press. Hay, David Ramsay. 1843. Proportion, or, The geometric principle
of beauty. Edinburgh: W. Blackwood. Herz-Fischler, Roger. 1984. Le Corbusier’s ‘Regulating
Lines’ for the Villa at Garches (1927) and Other Early Works. In: Journal of the
Society of Architectural Historians vol. 43, 1, p. 53–59. Herz-Fischler, Roger. 1997. Le Nombre d’or en France de 1886
à 1927. In: Revue de l’Art vol. 118, p. 9–16. Herz-Fischler, Roger. 1998. A Mathematical History of the Golden Number.
Mineola, NY: Dover. Hilpert, Thilo. 1999. Menschenzeichen. Ernst Neufert und Le
Corbusier. In: Walter Prigge, ed. Ernst Neufert: normierte Baukultur im 20.
Jahrhundert. Frankfurt/Main: Campus-Verlag, p. 131–143 (Edition Bauhaus, 5). Kidson, Peter. 1996. Architectural Proportion, § I: Before c.
1450. In: Jane Turner, ed. Dictionary of Art, vol. 2. New York: Grove, p.
343–353. Krier, Rob. 1992. Architectural composition. London: Academy
Press (first ed. 1988). Kroll, Johann F. 1839. Grundriß der Mathematik für
Gymnasien und andere höhere Lehranstalten. Eisleben: Reichardt. Le Corbusier-Saugnier. 1921.Les tracés régulateurs.
In: L’Esprit Nouveau vol. 5, p. 563–572. Le Corbusier. 1923. Vers une architecture. Paris: Cres et
Cie. Le Corbusier. 1948. Le Modulor. Boulogne-sur-Seine: Architecture
d’Aujoud’hui, Groupe Expansion. Le Corbusier. 1955. Modulor 2. Boulogne-sur-Seine: Editions
de L`Architecture d`Aujourd`hui. Lund, Fredrik Macody. 1921. Ad quadratum: A study of the geometrical
bases of classic & medieval religious architecture, London. Meckseper, Cord. 1983. Über die Fümfeckkonstruktion bei
Villard de Honnecourt und im späten Mittelalter. In: architectura vol. 13, p.
31–40. Mortet, Victor. 1911. Recueil de textes relatifs à l'histoire de
l'architecture et à la condition des architectes en Frances, au Moyen Age XIe et XIIe
siècles. Paris: Picard. Neufert, Ernst. 1936. Bauentwurfslehre. Berlin: Bauwelt-Verlag. Neufert, Ernst. 1941. Oktameter-System. Maßgrundlage für
Rohbau, Ausbau und Einrichtung unter Berücksichtigung geeigneter Steinformate. Berlin. Neufert, Ernst. 1943. Bauordnungslehre. Berlin: Volk und Reich Verlag. Ohm, Martin. 1835. Die reine Elementar-Mathematik. Berlin: Jonas. Ostwald,
Michael J. 2000. Under Siege: The Golden Mean in Architecture
In: Nexus Network Journal: Architecture and Mathematics vol. 2, p. 75–81. Pacioli, Luca. 1509. Divina proportione. Venice: Paganinus de Paganinis. Rpt. 1969. Urbino: Istituto Statale d’Arte. Pacioli, Luca. 1889. Divina Proportione. Die Lehre vom Goldenen Schnitt.
Nach der venezianischen Ausgabe vom Jahre 1509 neu ed., übersetzt und erläutert von
Constantin Winterberg, Vienna: Graeser (Quellenschriften für Kunstgeschichte und Kunsttechnik
des Mittelalters und der Neuzeit, N. F., 2). Padovan,
Richard. 1999. Proportion: Science, Philosophy, Architecture.
London:E & FN Spon. Palladio, Andrea. 1570. I quattro libri dell'architettura. Venice:
Franceschi. Pfeifer, Franz Xaver. 1885. Der goldene Schnitt und dessen
Erscheinungsformen in Mathematik, Natur und Kunst. Augsburg: Hattler. Philandrier, Guillaume. 1544. In decem libros M. Vitruuij Pollionis
de architectura adnotationes. Rome: Ioannes Andreas Dossena. Rackusin, Byrna. 1977. The architectural theory of Luca Pacioli: De
divina proportione, chapter 54. In: Bibliothèque d'Humanisme et Renaissance vol. 39,
p. 479–502. Rupprich, Bernhard, ed. 1956/1966/1969. Dürers schriftlicher
Nachlaß, 3 vols. Berlin: Deutscher Verein für Kunstwissenschaft. Schmidt, Carl. 1849. Proportionsschlüssel. Neues System der
Verhältnisse des menschlichen Körpers. Stuttgart. Scholfield, Paul H. 1958. The Theory of Proportion in Architecture.
Cambridge MA: Cambridge University Press. van der Schoot, Albert. 1997. De ontstelling van Pythagoras. Over
de geschiedeneis van de goddelijke proportie. Baarn (Netherlands): Kok Agora. Serlio, Sebastiano. 1537. Regole generali di architettura sopra le cinque
maniere degli edifici. Venice: Marcolini da Forlì. Serlio, Sebastiano. 1545. Il Primo libro d'architettura. Paris: Barbé. Serlio, Sebastiano. 1619. Tutte l'opere d’archittetura et
prospettiva di Sebastiano Serlio Bolognese. Venice: Giacomo de’Franceschi. Repr. 1964.
Ridgewood, NJ: Gregg. Serlio, Sebastiano. 1996/2001. Sebastiano Serlio on Architecture,
vol. I, Books I–V of 'Tutte l'opere d'architettura et prospettiva', translated from the
Italian with an Introduction and Commentary by Vaughan Hart and Peter Hicks, 2 vols. New Haven,
London: Yale University Press. Villard d’Honnecourt: see Hahnloser, Hans R. Vitruvius.
1969-2004. De architectura libri decem / De l’architecture, critical text
with French translation, 10 vols. Paris: Les Belles Lettres (Collection des Universités
de France, publieé sous la patronage de l’Association Guillaume Budé). Wesenberg, Burkhardt. 1983. Beiträge zur Rekonstruktion griechischer
Architektur nach literarischen Quellen. Berlin: Gebr. Mann Verlag (Mitteilungen des
Deutschen Archäologischen Instituts, Abt. Athen, 9. Beih.). Wiegand, August. 1849. Der allgemeine goldene Schnitt und sein
Zusammenhang mit der harmonischen Teilung. Halle: H. W. Schmidt. Wolff, Ferdinand. 1833. Lehrbuch der Geometrie. Berlin: Reimer. Zeising, Adolf. 1854. Neue Lehre von den Proportionen des menschlichen
Körpers aus einem bisher unerkannt gebliebenen, die ganze Natur und Kunst durchdringenden
morphologischen Grundgesetze entwickelt und mit einer vollständigen historischen Uebersicht der
bisherigen Systeme begleitet. Leipzig: Weigel. Zeising, Adolf. 1884. Der goldene Schnitt. Halle: Engelmann. About the autor Marcus
Frings is architectural theorist and art historian. He is Visiting
Associate Professor for Architectural History and Theory of Texas
A&M University in the Study Abroad Program. 2003-2005 he was Professor
at the University of Applied Sciences in Münster (Germany). 1996-2002
he was research assistant and lecturer for art history at Darmstadt
University of Technology (Germany), where in 1995 he was awarded
the doctor's degree with a thesis on the architectural theory of
the Italian Renaissance. His research interests are architecture,
iconography and the new media in art historical teaching and researching.
He is also trained in church-painting and restoration and worked
as consultant in historical monuments in a regional Chamber of
Handicrafts. He studied art history in Bonn and Berlin and completed
his thesis in Rome. For more information visit his homepage (www.marcus-frings.de).
1 Based mainly on Vitruvius and some observations in buildings, Wesenberg supposes that the completely lost syngraphe writings (or commentarii in Vitruvius’ words) described measures and proportions of certain temples a posteriori; that is, the architects published their own data of planning in written form, not as drawings. Only in Hellenistic times emerges a kind of literature with a more theoretical character, called praecepta, which publish examples of ideal designs in written form too, reflecting the principal questions that Vitruvius later considers.
2 Translated by the present author from [Vitruvius 1990: 6]: "Namque non potest aedes ulla sine symmetria atque proportione rationem habere compositionis, nisi uti [ad] hominis bene figurati membrorum habuerit exactam rationem."
3 Anthropos and mimesis: a mimetic imitation of the body.
4 Two manuscripts dated 1498 contain 60 drawings of Leonardo da Vinci: Geneva, Bibliothèque Publique et Universitaire, Cod. 250, and Milan, Biblioteca Ambrosiana, Ms. E 170 sup., the last one published as édition de luxe on hand-made paper fully illustrated 1956 in Milan (Fontes Ambrosiani, 31).
5 Examples given in [Daly Davis 1977: 98, n. 2].
6 So his Divina proportione has been mocked as "ceneraccio" (ash-sewage) in sources cited by Winterberg [Pacioli 1889: 13].
7 I, f. 23r: "Ex Venetiis kal. Maii. M.D.VIII.", but from the dating in the seventh year of the pontificate of Alexander VI it would be 1498. He puts it in the "pars prima" of Divina proportione, but begins to count new chapters with it.
8 I, f. 23r: "degni lapicidi de scultura e architectonica faculta solertissimi sectatori……alcuna norma e modo a poter conseguire el vostro disiato effecto delarchitectura."
9 I,8, f. 29v. However he mentions Alberti only to rebuke his Tuscan companion to speak of an order “Italiche” rather than "Tuscane".
10 I,7, f. 29r: "malenconica e flebile vidouile…giouine polite alegre e ... piu legiadria".
11 Paris, Bibliothèque Nationale, fonds français, 19093, f. 18v; the plate cited is still the best illustration.
12 Divina proportione I,54, f. 16r: "benche nol sapino ... Ancora el sarto e calzolaro vsano la geometria e non sanno che cosa sia. El si murari legnaoli fabri e ogni artefici vsano le mesura e la proportione e non sanno. Peroche commo altre volte e detto tutto consiste nel numero peso e mesura. ... e poi nelle fabriche non regano il peso ... ruinano."
13 Rackusin [1977] thinks too highly of this chapter as "in actuality a miniature architectural treatise" (p. 479) and cannot prove here remarks on the number-symbolism of 72 for Pacioli.
14 Divina proportione I,18, f. 32v: "Comme lapicidi e altri scultori in dicti corpi sieno commendati."
15 Ib.: "ve ricordo che non siranno da biasimare le vostre opere se a le volte ... vi poneste o per basa o capitelli qualcuno de quelli nostri corpi mathematici ... Anze siranno de dignissima commendatione del vostro opifitio per che non solo lo rendaranno adorno ma ancora ali docti e spaienti daranno da speculare conciosia che sempre sieno fabricati con quella sancta e divina proportione hauente medium duoque extrema etc."
16 Divina proportione I,19, f. 32v.: "E se non potrete in tutto farle a tutto quadrato over circulo prendarete di loro sempree qualche parte over parti nota over note comme a dire la 1/2 el 1/3 li 3/4 li 2/3 et cetera o aloro circuito overo diametri, e quelli proportionando sempre quanto piu potrete in parti note che per numero si possano mostrare. Se non con stretti da la irrationalita comme fra el diametro del quadro e sua costa. Alora segnarete con vostra squadra e sexto lor termini in linee con vostro desegno. Peroche avenga che non sempre per numero se possino nominare ma mai sia impedito che per linea superficie non se possino assegnare. Conciosia che la proportione sia molto piu ampla in la quantita continua che in la discreta."
17 So still Peter Kidson [1996: 345].
18 Regole generali f. 3v. The new Hart and Hicks translation identifies the square root wrongly with the Golden Section throughout; see [Serlio 1996/2001: 431, n. 56; 449, n. 56; 450, n. 115].
19 In the Parisian Codex, between 1487 and 1497 (Ms. A f. 13v, Ms. B f. 13v, Ms. B f. 27v), and in the Codex Atlanticus, ca.1508 (f. 362 r–b), see [Meckseper].
20 E.g. the London leaves c. 1513 [Rupprich 1956/1966/1969: n. 12, n. 16, n. 17]; see [Fredel: 1998].
21 On the philosophical backgound concentrates Albert van der Schoot [1997: 179–200].
22 This is not to be confused with the small, posthumuously compiled paper Der goldene Schnitt [Zeising: 1884].
23 [Zeising 1854: 389]; Darwin’s theory of evolution had not been published yet, but was already — with others — in discussion.
24 [Schmidt 1849]; following him Zeising [1854] designed his fig. 2, p. 85. Furthermore he illustrates [Hay 1843], cf. [Zeising 1854: fig. 1, p. 63] and [Carus 1853], cf. [Zeising 1854: fig. 3, p. 95].
25 Carefully considered already in [Scholfield 1958: 98]: "A fairly good case could be made out for the view that the nineteenth century actually discovered the golden section as an instrument of architectural proportion".
26 Still in Zeising’s lifetime [Bochenek 1875], then e.g. [Goeringer 1893] or [Pfeifer 1885].
27 See, for example, [Lund 1921; Hambidge 1920; Funck-Hellet 1951; up to Doczi 1996].
28 With [Fechner 1865] and varying exposition and reflection [Fechner 1876].
29 On the other hand Dessoir [1906: 124–127], and Borissavlievitch [1954] discuss the Golden Section critically.
30 Most famously [Cook 1922], and more recently [Ostwald 2000].
31 Here the influence of Otto Bartning is probable, who advised Neufert in this part.
32 In 1921 Le Corbusier had published as Le Corbusier-Saugnier, Les tracés régulateurs.
33 Le Corbusier himself presents the façades with rectangular "tracé regulateur"; cf. [Herz-Fischler 1984].